問題
ABC284 F - ABCBAC
お気持ち
- そもそも問題を理解するのが難しい
- 「文字列Sの先頭i文字 + 文字列Sを反転したやつ + 文字列Sの末尾N-i文字」が、Tと一致するならiとSを出力
- 文字列Sを2つ用意してそれぞれA、Bとするじゃん?
- 文字列Aを適当にぶっちぎるじゃん?(A1,A2)
- 文字列Bは反転させるじゃん?
- A1,B,A2 = Tになるようなちぎり方はありますか?って聞かれてる
- 制約はそんなに大きくはないけど、$N^2$は無理。つむつむ。
- Aをちぎる箇所を全探索して、全部ひっつけたものがTになるかを一個ずつ比較していけばそれで済むけどそんなことは当たり前のように許されない
- とりあえずokkuu氏に教えてもらった典型テクとして、
- 文字列の逆順が関係してくる文字列系の問題では、元の文字列とその逆順をくっ付けたやつに文字列アルゴリズムを行う
- 文字列Tと、文字列Tの反転をくっつける。
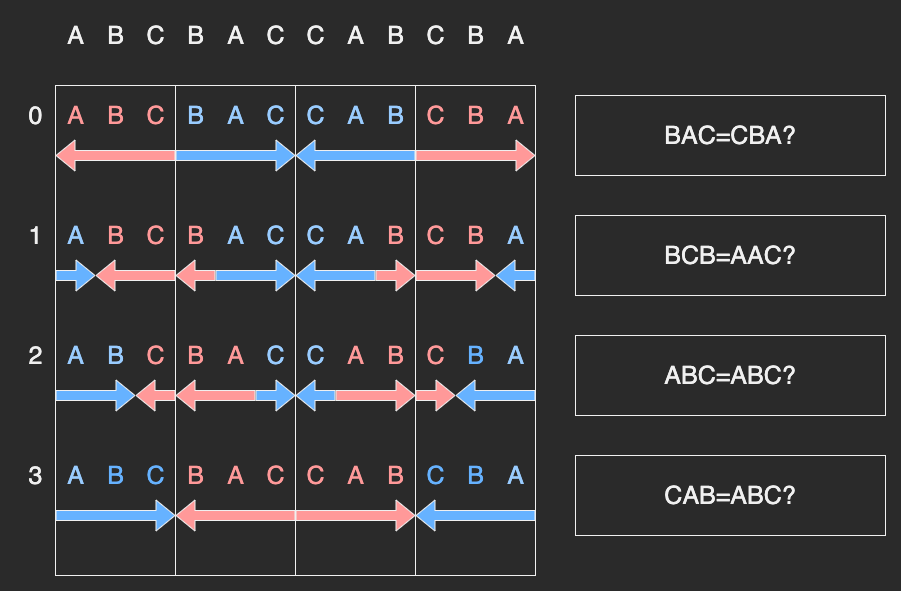
- 後は長さの同じ右向きの赤矢印、青矢印をそれぞれ比較していって全部OKなら成立する、という話
- これで文字列いちいち結合しなくても良くなった!素敵!
- ただ、長い文字列を何回も比較するのはちょっと計算量的にやなので、ローリングハッシュ使う
- 前準備が必要だけどO(1)で部分文字列の比較が出来る凄いやつ!強い!
ソースコード
class RollingHash():
def __init__(self, s, base=37, mod=(1 << 61) - 1):
self.mask30 = (1 << 30) - 1
self.mask31 = (1 << 31) - 1
self.mod = mod
self.base = base
self.mask61 = (1 << 61) - 1
self.positivizer = self.mod * ((1 << 3) - 1)
l = len(s)
self.pw = pw = [1] * (l + 1)
self.h = h = [0] * (l + 1)
v = 0
for i in range(l):
self.h[i + 1] = v = self.calcmod(self.mul(v, base) + ord(s[i]))
v = 1
for i in range(l):
self.pw[i + 1] = v = self.calcmod(self.mul(v, base))
def get(self, start, length):
return self.calcmod(self.h[start + length] + self.positivizer - self.mul(self.h[start], self.pw[length]))
def mul(self, a, b):
au = a >> 31
ad = a & self.mask31
bu = b >> 31
bd = b & self.mask31
mid = ad * bu + au * bd
midu = mid >> 30
midd = mid & self.mask30
return self.calcmod(au * bu * 2 + midu + (midd << 31) + ad * bd)
def calcmod(self, x):
xu = x >> 61
xd = x & self.mask61
res = xu + xd
if res >= self.mod:
res -= self.mod
return res
N = int(input())
T = input()
T = T + T[::-1]
rh = RollingHash(T)
for i in range(N + 1):
if rh.get(0, i) == rh.get(3 * N - i, i) and rh.get(N + i, N - i) == rh.get(3 * N, N - i):
print(T[3 * N - i:4 * N - i])
print(i)
exit()
print(-1)
